A PD or PID controller is probably the most commonly used type for micromouse motor control. It is not the only way to get the job done though. An alternative is the phase-lead controller. This is the kind of controller described by David Otten in his Circuit Cellar articles…
One of the disadvantages of a PD controller is its sensitivity to noise. If you are using encoders to measure position, they are inherently noisy. Although the encoder output is digital, the noise, as far as the control system is concerned, comes from the discrete steps in the output. You cannot measure a fraction of an encoder count. That can be seen in the responses of the PD controller described in the earlier post. There you can see that the PWM output jumps around quite a lot. This is, I believe, due to the effect of the D term in the controller responding to those discrete changes in the encoder values.
A phase lead controller can smooth these out at the cost of a slightly more complex controller. The differences are small though and worth the trouble. Again, I am not a control engineer so I have no detailed explanation to offer, only a way to design and implement such a controller.
As with the PD controller, you will need to determine the system characteristics before starting. A way to do that is described here. For the examples on this post, I will use the same test rig as for the PD controller so that they can be directly compared. This consusts of a Faulhaber 1717SR006 motor with 512 count encoder attached. A steel disk is attached to the motor shaft, presenting a similar load to that seen by a light micromouse. The transfer function for the system is:
![]()
The DC, or steady-state, gain is Km = 142 and the time constant, Tm is 0.165 seconds. As a reminder, this means that a PWM input of 500 would cause the motor to turn at a speed of 71,000 counts per second – 8300 rpm. In practice it would be a bit less than that due to friction losses. It would take the motor 0.165 seconds to reach 63% of that value – a fairly slow response.
Normally, most sources would now have you reach for Matlab to model the system and perform various mysterious acts to turn it into a good control system. If, like me, you cannot pay for Matlab and the open source equivalent – Octave – is pretty mysterious in itself, you will have to find another way.
Like the PD controller, we can define the closed loop system in terms of some of its open-loop characteristics. The key values are the system bandwidth, which describes how rapidly it can respond to change, and its phase margin which describes how stabe it will be when the control loop is closed.
For this example, I shall choose the bandwidth, ωc, to be 80 radians per second. This is a similar value to that I ended up with in the PD controller. At its simplest, rise time is the time taken for the system to get from 10% to 90% of its output after a step change. For now, consider that the rise time is about 1.8/ωc where ωc is in radians per second. Thus a bandwidth of 80 rad/sec would give us a rise time of about 22ms.
The phase margin, ![]() , is about stability and overshoot and is related to the damping factor,
, is about stability and overshoot and is related to the damping factor, ![]() , chosen in the PD controller. Suffice it to say that, for the position controller, a phase margin of 45 degrees will suitable for our needs.
, chosen in the PD controller. Suffice it to say that, for the position controller, a phase margin of 45 degrees will suitable for our needs.
If you want to find out how this stuff really works, you might want to start at the University of Michigan and branch out.
Meantime, I have two key parameters – bandwidth, ![]() = 80 rad/sec and phase margin,
= 80 rad/sec and phase margin, ![]() = 45 degrees.
= 45 degrees.
Now for the sums. I have no intention of explaining how these are derived – there are plenty of good sources out there. I owe a lot to help from Dave Otten and Harjit Singh.
My mouse runs its control loop at 1kHz so the sample time, ![]() is 0.001 seconds.
is 0.001 seconds.
The controller is described by the following equation:
![]()
I need to find values for ![]() ,
,![]() and
and ![]() .
.
The existing system will already have a gain and phase corresponding to the chosen bandwidth. I need to know what those are so that I can adjust them with the controller. The gain at my chosen bandwidth is:
![]()
And the corresponding phase is:
![]()
The phase calculated will almost certainly be less than that required by my specification so I want the controller to add an extra phase (hence the term phase lead) to the system. The amount is simply:
![]()
That value is used to calculate a working variable ![]()
![]()
Then I use that to obtain values for ![]() and
and ![]()
![]()
![]()
The gain, Kc, is that required to restore the attenuation of the other parts of the filter so first, I need to find out the gain of the controller at the corner frequency (bandwidth)
![Rendered by QuickLaTeX.com \[G_c=\frac{\sqrt{1+T_Z^2\omega_c^2}}{\sqrt{1+T_P^2\omega_c^2}}\]](https://micromouseonline.com/wp-content/ql-cache/quicklatex.com-ad0845b4791a8b74b341560e0ed04184_l3.png)
Now the restoring gain can be calculated from:
![]()
By now, you are probably on the verge of giving up. Don’t – it all works out in the end.
The controller transfer function can be turned into a single line of code by the magic of z-transforms and the like. The code for the controller is pretty simple
errorOld = error; error = setPos - currentPos;
PWMOld = PWM; PWM = K1 * error - K2 * errorOld + K3 * PWMOld;
Notice that the controller acts not only on the error and the previous error but also takes into account the previous output.
The three constants, ![]() ,
, ![]() and
and ![]() , can be calculated fom the values of
, can be calculated fom the values of ![]() ,
, ![]() and
and ![]() :
:
![]()
![]()
![]()
In practice, the constants all work out to be fractional values. Rather than use floating point in the controller code, I multiply each by 256 and then divide the output by 256 again to get whole numbers. Remember to round to the nearest integer value to prevent cumulative errors.
For the test rig I get a code fragment that looks like this:
long K1 = 4087; long K2 = 3948; long K3 = 213; errorOld = error; error = setPos - currentPos; PWMOld = PWM; PWM = (K1*error - K2*errorOld + K3*PWMOld + 128)/256;
That was a lot of work. How well does it perform? Here is the result of a single step from 0 to 256 counts. Exactly the same requested step as was used for the PD controller. On this graph, the phase lead controller is shown in green and the PD controller data is shown for comparison in red.
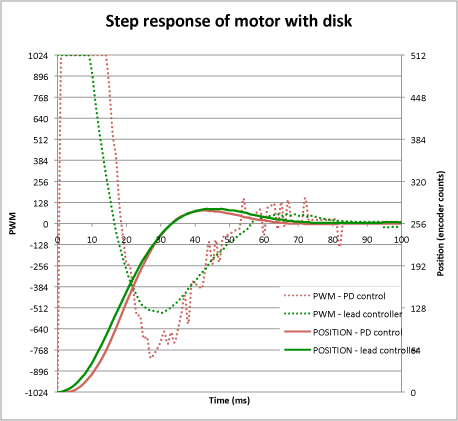
Note that, for the PD controller, in order to get a similar response to the lead controller, I had to increase the gain by 60% over the value calculated in the previous post. Both controllers get to their target in about the same time but the lead controller is clearly generating smoother PWM outputs. This is a feature of the controller and should make both the motor and the motor drivers work a bit less hard for appreciably the same results.
If you are, understandably, put off from using this type of controller because all the maths made your ears bleed, you might want to have a go at the attached spreadsheet where you can fill in the system parameters and your desired margin and bandwidth. The spreadsheet will calculate all the hard stuff for you.
Thank you for sharing with us such a valuable experience in designing phase-lead controllers.
Are you using Trapesoid Rule to replace the variable s with 2(z-1)/Ts(z+1)?
I tried to double check the formulas for K1, K2, and K3 with trapesoid rule, but I found that
K1 = Kc(2Tz+Ts)/(2Tp+Ts) which is the same as yours
K2 = Kc(2Tz-Ts)/(2Tp+Ts) <– not the same
K3 = (2Tp-Ts)/(2Tp+Ts) <– not the same
Did I misunderstand what you meant?
Thank you for looking at this.
You are quite right and I have changed the post to correct the error. There was only one error – the equation for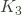 – where I had the sign of the numerator wrong. For the second equation, I had used
– where I had the sign of the numerator wrong. For the second equation, I had used 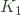 as the multiplier rather than
as the multiplier rather than 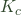 but it works out the same either way. The revised version above shows both but you were, of course, quite right for the expression you gave for
but it works out the same either way. The revised version above shows both but you were, of course, quite right for the expression you gave for 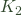 .
.
I would be interested to find out how you get on with an actual implementation. Your comment made me go back and look over my work and I think I now understand why my mouse will not corner properly. I made a (different) error in the calculation of the phase lead compensator for the rotational controller. Hopefully, I can get it working properly now.
Pingback: 數位相位超前控制器心得 | 嵌入式控制系統實驗室
Hello Peter,
I really appreciate all the work you put to share your experience with the world.
I’m currently working on my micromouse robot and I’m having quite a problem with driving the motors. Today I tried to use the method described on this page, but it went rather wrong, as I got the values of K1,2,3 accordingly: 17812.4076603 10.5894018718 244.56634477 (without multiplying) and it obviously didn’t work out.
But the main problem I seem to have problems with is combining two controllers to work together. What you describe here is controlling just a single motor. But could you tell me how to use it in a system built using two profilers – for transaltion and rotation?
Thanks in advance for any help 😉
Hello again Peter,
I hope the All Japan tournament went well!
This article references a spreadsheet that seems to be missing. Is there a way that
you could reupload that spreadsheet?
Thank you!
Don’t know what happened to that! You will find it linked at the bottom of the post now.
Thanks!
It is very useful in understanding the article. However, there was a discrepancy between
the zero and pole time constant in the spreadsheet vs the article. Could you point out which
one is correct?
I just checked the spreadsheet against a known good solution and it gave good answers. I say good rather than correct as the original uses a modelling tool and I think that the spreadsheet gives values close enough (within 1%) to those given by the other tool that I think the answers are still valid. Most likely, the modelling tool probably knows the initial parameters to a better precision than I do.
So,it looks like I put bits from a slightly different problem in the text. I will check it through again but, for now, the spreadsheet gives the right answer as far as I can tell.