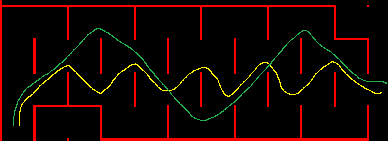
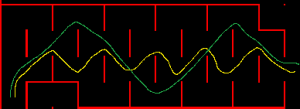
If the maze has a region as shown on the left, and the mouse enters the region on the bottom left and exits on the right side, which path will your solver generate for the mouse?
Introduction
The Zeetah series of mice use a orthogonal move based maze solver which was written between 1987 and 1989. An orthogonal solver finds paths through the maze assuming the mouse can make inplace 90 degree turns and it can accelerate/decelerate down long straights.
What this means from a practical point of view is that, there is one and only one time (cost) used for turns and then there is a table that has a list of times for straights. The time in this table is calculated based on an particular set of motion parameters – acceleration/deceleration/maximum velocity profile. This means that two one cell moves have a higher time than one two cell move since the two one cell moves involve the mouse accelerating, decelerating and then accelerating and decelerating. Whereas the one two cell command has the mouse do one acceleration phase and then one deceleration phase.
To support diagonal motion, after an orthogonal path is known, the path is run through a routine that converts the orthogonal path to one that includes diagonals.
The orthogonal solver is very attractive because it requires very little RAM – in my implementation it needs around 1K to 2K of RAM, it executes very quickly (3ms unoptimized ARM Cortex M3) and the code size is small – on the order of several hundred bytes. The disadvantage is that the path is usually not the optimal path. For example, in the image shown below, assume the mouse enters from the bottom left and exits on the right hand side, what is the best path through the region?
I’ve seen the orthogonal solver take the yellow path which is much slower than the green path because of the excessive number of diagonal to diagonal 90 degree turns.
Given that contests are being won and lost in the tens of milliseconds range, it is time (no pun intended) to generate a path that has appropriate time for all turn types.
With mice having become much faster, another trend that has emerged is that orthogonal straights, diagonal straights and turns are run with different motion parameters than diagonals (Koji Mouse Run Parameters). Also, all turns don’t have the same acceleration. While it would have been nice to have taken these factors into account, it is to be determined whether the final implementation will do so.
To make coding and implementation easier, the initial strategy is to not optimize any of the data structures or code. Once the diagonal solver is working and more insight has been gained about the solution and the implementation, then optimizations will be made.
Flooding
The diagram below shows all the combinations for the current motion command and the next motion commands.
The flooding routine will get a coordinate from the Expand queue and then using the information in the maze structure and the expansion rules shown below, it will compute the time and if necessary, update the maze structure and add the cell to the Expand queue.
In the next installment, I’ll share the data structures and more specifics on the algorithm.
NOTE from admin:
This article is also available translated to Serbo-Croatian language by Jovana Milutinovich from Webhostinggeeks.com.